Structural requirements
|
|
1. Introduction
To perform its function of supporting a building in response to whatever loads may be applied to it, a structure must possess four properties: it must be capable of achieving a state of equilibrium, it must be stable, it must have adequate strength and it must have adequate rigidity. The meanings of these terms are explained in this chapter. The influence of structural requirements on the forms which are adopted for structures is also discussed. The treatment is presented in a non-mathematical way and the definitions which are given are not those of the theoretical physicist; they are simply statements which are sufficiently precise to allow the significance of the concepts to structural design to be appreciated.
2. Equilibrium
Structures must be capable of achieving a state of equilibrium under the action of applied load. This requires that the internal configuration of the structure together with the means by which it is connected to its foundations must be such that all applied loads are balanced exactly by reactions generated at its foundations. The wheelbarrow provides a simple demonstration of the principles involved. When the wheelbarrow is at rest it is in a state of static equilibrium. The gravitational forces generated by its self weight and that of its contents act vertically downwards and are exactly balanced by reacting forces acting at the wheel and other supports. When a horizontal force is applied to the wheel barrow by its operator it moves horizontally and is not therefore in a state of static equilibrium.This occurs because the interface between the wheelbarrow and the ground is incapable of generating horizontal reacting forces. The wheelbarrow is both a structure and a machine: it is a structure under the action of gravitational load and a machine under the action of horizontal load.
Despite the famous statement by one celebrated commentator, buildings are not machines1. Architectural structures must,therefore, be capable of achieving equilibrium under all directions of load.
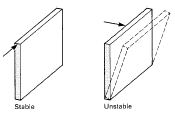
3. Geometric stability
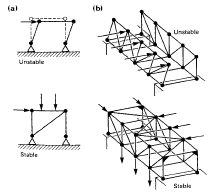
Geometric stability is the property which preserves the geometry of a structure and allows its elements to act together to resist load. The distinction between stability and equilibrium is illustrated by the framework shown in Fig. 2.1 which is capable of achieving a state of equilibrium under the action of gravitational load. The equilibrium is not stable, however, because the frame will collapse if disturbed laterally2.
Fig. 2.1 A rectangular frame with four hinges is capable
of achieving a state of equilibrium but is unstable because
any slight lateral disturbance to the columns will induce it
to collapse. The frame on the right here is stabilised by the
diagonal element which makes no direct contribution to
the resistance of the gravitational load.
This simple arrangement demonstrates that the critical factor, so far as the stability of any system is concerned, is the effect on it of a small disturbance. In the context of structures this is shown very simply in Fig. 2.2 by the comparison of tensile and compressive elements. If the alignment of either of these is disturbed, the tensile element is pulled back into line following the removal of the disturbing agency but the compressive element, once its initially perfect alignment has been altered, progresses to an entirely new position. The fundamental issue of stability is demonstrated here, which is that stable systems revert to their original state following a slight disturbance whereas unstable systems progress to an entirely new state.
The parts of structures which tend to be unstable are the ones in which compressive forces act and these parts must therefore be given special attention when the geometric stability of an arrangement is being considered. The columns in a simple rectangular framework are examples of this(Fig. 2.1). The three-dimensional bridge structure of Fig. 2.3 illustrates another potentially unstable system. Compression occurs in the horizontal elements in the upperparts of this frame when the weight of an object crossing the bridge is carried. The arrangement would fail by instability when this load was applied due to inadequate restraint of these compression parts. The compressive internal forces, which would inevitably occur with some degree of eccentricity, would push the upper elements out of alignment and cause the whole structure to collapse.

because the loads pull it back into line following a disturbance.
The compressive element on the right is fundamentally unstable.
Fig. 2.3 The horizontal elements in the tops of the bridge girders
are subjected to compressive internal force when the load is applied.
The system is unstable and any eccentricity which is present initially
causes an instability-type failure to develop.
The geometric instability of the arrangements in Figures 2.1 and 2.3 would have been obvious if their response to horizontal load had been considered (Fig. 2.4).This demonstrates one of the fundamental requirements for the geometric stability of any arrangement of elements, which is that it must be capable of resisting loads from orthogonal directions (two orthogonal directions for plane arrangements and three for three-dimensional arrangements). This is another way of saying that an arrangement must be capable of achieving a state of equilibrium in response to forces from three orthogonal directions. The stability or otherwise of a proposed arrangement can therefore be judged by considering the effect on it of sets of mutually perpendicular trial forces: if the arrangement is capable of resisting all of these then it is stable, regardless of the loading pattern which will actually be applied to it in service. Conversely, if an arrangement is not capable of resisting load from three orthogonal directions then it will be unstable in service even though the load which it is designed to resist will be applied from only one direction.
(a) The two-dimensional system is stable if it is capable of achieving equilibrium in response to forces from two mutually perpendicular directions.
(b) The three-dimensional system is stable if it is capable of resisting forces from three directions. Note that in the case illustrated the resistance of transverse horizontal load is achieved by the insertion of rigid joints in the end bays.
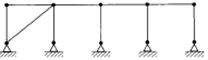
It frequently occurs in architectural design that a geometry which is potentially unstable must be adopted in order that other architectural requirements can be satisfied. For example, one of the most convenient structural geometries for buildings, that of the rectangular frame, is unstable in its simples thing e-jointed form, as has already been shown.Stability can be achieved with this geometry by the use of rigid joints, by the insertion of a diagonal element or by the use of a rigid diaphragm which fills up the interior of the frame (Fig. 2.5). Each of these has disadvantages. Rigid joints are the most convenient from a space-planning point of view but are problematic structurally because they can render the structure statically indeterminate (see Appendix 3). Diagonal elements and diaphragms block the frame work and can complicate space planning. In multi-panel arrangements, however, it is possible to produce stability without blocking every panel.The row of frames in Fig. 2.6, for example, is stabilised by the insertion of a single diagonal.
Fig. 2.5 A rectangular frame can be stabilised
by the insertion of (a) a diagonal element or (b) a rigid
diaphragm, or (c) by the provision of rigid joints.
A single rigid joint is in fact sufficient to provide stability.
Fig. 2.6 A row of rectangular frames is stable if one panel
only is braced by any of the three methods shown in Fig. 2.5.
Where frames are parallel to each other the three-dimensional arrangement is stable if a few panels in each of the two principal directions are stabilised in the vertical plane and the remaining frames are connected to these by diagonal elements or diaphragms in the horizontal plane (Fig. 2.7). A three-dimensional frame can therefore be stabilised by the use of diagonal elements or diaphragms in a limited number of panels in the vertical and horizontal planes. In multi-storey arrangements these systems must be provided at every storey level.
Fig. 2.7 These frames containt he minimum
number of braced panels required for stability.
None of the components which are added to stabilise the geometry of the rectangular frame in Fig. 2.7 makes a direct contribution to the resistance of gravitational load (i.e. the carrying of weight, either of the structure itself or of the elements and objects which it supports). Such elements are called bracing elements. Arrangements which do not require bracing elements, either because they are fundamentally stable or because stability is provided by rigid joints, are said to be self-bracing.
Most structures contain bracing elements whose presence frequently affects both the initial planning and the final appearance of the building which it supports. The issue of stability, and in particular the design of bracing systems, is therefore something which affects the architecture of buildings.
Where a structure is subjected to loads from different directions, the elements which are used solely for bracing when the principal load is applied frequently play a direct role in resisting secondary load. The diagonal elements in the frame of Fig. 2.7, for example,would be directly involved in the resistance of any horizontal load which was applied, such as might occur due to the action of wind. Because real structures are usually subjected to loads from different directions, it is very rare for elements to be used solely for bracing.
The nature of the internal force in bracing components depends on the direction in which the instability which they prevent occurs. In Fig. 2.8, for example, the diagonal element will be placed in tension if the frame sways to the right and in compression if it sways to the left. Because the direction of sway due to instability cannot be predicted when the structure is being designed, the single bracing element would have to be made strong enough to carry either tension or compression. The resistance of compression requires a much larger size of cross-section than that of tension, however,especially if the element is long3, and this is a critical factor in determining its size. It is normally more economical to insert both diagonal elements into a rectangular frame (cross-bracing) than a single element and to design both of them as tension-only elements.When the panel sways due to instability the element which is placed in compression simply buckles slightly and the whole of the restraint is provided by the tension diagonal.

caused by instability is always resisted by a diagonal
element acting in tension. The compressive diagonal
buckles slightly and carries no load.
It is common practice to provide more bracing elements than the minimum number required so as to improve the resistance of three-dimensional frameworks to horizontal load. The framework in Fig. 2.7, for example,although theoretically stable, would suffer considerable distortion in response to a horizontal load applied parallel to the long side of the frame at the opposite end from the vertical-plane bracing. A load applied parallel to the long side at this end of the frame would also cause a certain amount of distress as some movement of joints would inevitably occur in the transmission of it to the vertical-plane bracing at the other end. In practice the performance of the frame is more satisfactory if vertical-plane bracing is provided at both ends (Fig. 2.9). This gives more restraint than is necessary for stability and makes the structure statically in determinate (see Appendix 3), but results in the horizontal loads being resisted close to the points where they are applied to the structure.Another practical consideration in relation to the bracing of three-dimensional rectangular frames is the length of the diagonal elements which are provided. These sag in response to their own weight and it is therefore advantageous to make them as short as possible. For this reason bracing elements are frequently restricted to a part of the panel in which they are located. The frame shown in Fig. 2.10 contains this refinement.
Fig. 2.9 In practical bracing schemes more elements
than are strictly necessary to ensure stability are provided
to improve the performance of frameworks in resisting
horizontal load. Frame (a) is stable but will suffer distortion
in response to horizontal load on the side walls.Its performance
is enhanced if a diagonal element is provided in both end walls
(b). The lowest framework (c)contains the minimum number of elements
required to resist effectively horizontal load from the two principal horizontal
directions. Note that the vertical-plane bracing elements are
distributed around the structure in asymmetrical configuration.
Fig. 2.10 In practice, bracing elements are
frequently confined to a part of each panel only.
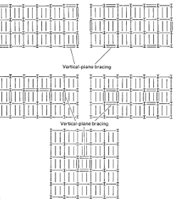
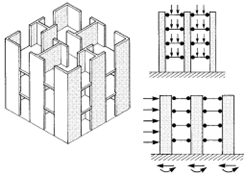
Figures 2.11 and 2.12 show typical bracing systems for multi-storey frameworks. Another common arrangement, in which floor slabs act as diaphragm-type bracing in the horizontal plane in conjunction with vertical-plane bracing of the diagonal type, is shown in Fig.2.13. When the rigid-joint method is used it is normal practice to stabilise all panels individually by making all joints rigid. This eliminates the need for horizontal-plane bracing altogether, although the floors normally act to distribute through the structure any unevenness in the application of horizontal load. The rigid-joint method is the normal method which is adopted for reinforced concrete frames, in which continuity through junctions between elements can easily be achieved; diaphragm bracing is also used, however, in both vertical and horizontal planes in certain types of reinforced concrete frame.
Load bearing wall structures are those in which the external walls and internal partitions serve as vertical structural elements. They are normally constructed of masonry, reinforced concrete or timber, but combinations of these materials are also used. In all cases the joints between walls and floors are normally incapable of resisting bending action (in other words they behave as hinges) and the resulting lack of continuity means that rigid-frame action cannot develop. Diaphragm bracing,provided by the walls themselves, is used to stabilise these structures. concrete or timber, but combinations of these materials are also used. In all cases the joints between walls and floors are normally incapable of resisting bending action (in other words they behave as hinges) and the resulting lack of continuity means that rigid-frame action cannot develop. Diaphragm bracing,provided by the walls themselves, is used to stabilise these structures.
Fig. 2.11 A typical bracing scheme for a multi-storey
framework. Vertical-plane bracing is provided in a limited
number of bays and positioned symmetrically on plan.
All other bays are linked to this by diagonal bracing in
the horizontal plane at every storey level.
Fig. 2.12 These drawings of floor grid patterns for steel
frameworks show typical locations for vertical-plane bracing.
Fig. 2.13 Concrete floor slabs are normally used
as horizontal-plane bracing of the diaphragm type which
acts in conjunction with diagonal bracing in the vertical planes.
A wall panel has high rotational stability in its own plane but is unstable in the out-of-plane direction (Fig. 2.14); vertical panels must, therefore, be grouped in pairs at right angles to each other so that they provide mutual support. For this to be effective the structural connection which is provided in the vertical joint between panels must be capable of resisting shear4. Because load bearing wall structures are normally used for multi-cellular buildings, the provision of an adequate number of vertical-plane bracing diaphragms in two orthogonal directions is normally straight forward (Fig. 2.15). It is unusual therefore for bracing requirements to have a significant effect on the internal planning of this type of building.
Fig. 2.14 Walls are unstable in the out-of-plane direction and
must be grouped into orthogonal arrangements for stability.
Fig. 2.15 Load bearing masonry buildings are normally
multi-cellular structures which contain walls running in
two orthogonal directions. The arrangement is inherently stable.
The need to ensure that a structural framework is adequately braced is a factor that can affect the internal planning of buildings.The basic requirement is that some form of bracing must be provided in three orthogonal planes. If diagonal or diaphragm bracing is used in the vertical planes this must be accommodated within the plan. Because vertical-plane bracing is most effective when it is arranged symmetrically, either in internal cores or around the perimeter of the building,this can affect the space planning especially in tall buildings where the effects of wind loading are significant.
4. Strength and rigidity
4.1 Introduction
The application of load to a structure generates internal forces in the elements and external reacting forces at the foundations (Fig.2.16) and the elements and foundations must have sufficient strength and rigidity to resist these. They must not rupture when the peak load is applied; neither must the deflection which results from the peak load be excessive.
Fig. 2.16 The structural elements of a building conduct
the loads to the foundations. They are subjected to internal
forces that generate stresses the magnitudes of which depend
on the intensities of the internal forces and the sizes of the elements.
The structure will collapse if the stress levels exceed the strength of the material.
The requirement for adequate strength is satisfied by ensuring that the levels of stress which occur in the various elements of a structure, when the peak loads are applied, are within acceptable limits. This is chiefly a matter of providing elements with cross-sections of adequate size, given the strength of the constituent material. The determination of the sizes required is carried out by structural calculations. The provision of adequate rigidity is similarly dealt with.
Structural calculations allow the strength and rigidity of structures to be controlled precisely. They are preceded by an assessment of the load which a structure will be required to carry. The calculations can be considered to be divisible into two parts and to consist firstly of the structural analysis, which is the evaluation of the internal forces which occur in the elements of the structure, and secondly,the element-sizing calculations which are carried out to ensure that they will have sufficient strength and rigidity to resist the internal forces which the loads will cause. In many cases, and always for statically indeterminate structures (see Appendix 3), the two sets of calculations are carried out together, but it is possible to think of them as separate operations and they are described separately here.
4.2 The assessment of load
The assessment of the loads which will act on a structure involves the prediction of all the different circumstances which will cause load to be applied to a building in its lifetime (Fig.2.17) and the estimation of the greatest magnitudes of these loads. The maximum load could occur when the building was full of people, when particularly heavy items of equipment were installed, when it was exposed to the force of exceptionally high winds or as a result of many other eventualities. The designer must anticipate all of these possibilities and also investigate all likely combinations of them.
The evaluation of load is a complex process,but guidance is normally available to the designer of a structure from loadingstandards5. These are documents in which data and wisdom gained from experience are presented systematically in a form which allows the information to be applied in design.
Fig. 2.17 The prediction of the maximum load which will occur is one of the most problematic aspects of structural calculations. Loading standards are provided to assist with this but assessment of load is nevertheless one of the most imprecise parts of the structural calculation process.
4.3 The analysis calculations
The purpose of structural analysis is to determine the magnitudes of all of the forces,internal and external, which occur on and in a structure when the most unfavourable load conditions occur. To understand the various processes of structural analysis it is necessary to have a knowledge of the constituents of structural force systems and an appreciation of concepts, such as equilibrium, which are used to derive relationships between them. These topics are discussed in Appendix 1.
In the analysis of a structure the external reactions which act at the foundations and the internal forces in the elements are calculated from the loads. This is a process in which the structure is reduced to its most basic abstract form and considered separately from the rest of the building which it will support.
An indication of the sequence of operations which are carried out in the analysis of a simple structure is given in Fig. 2.18. After a preliminary analysis has been carried out to evaluate the external reactions, the structure is subdivided into its main elements by making ‘imaginary cuts’ (see Appendix 1.7) through the junctions between them. This creates a set of‘free-body-diagrams’ (Appendix 1.6) in which the forces that act between the elements are exposed. Following the evaluation of these inter-element forces the individual elements are analysed separately for their internal forces by further applications of the ‘imaginary cut ’technique. In this way all of the internal forces in the structure are determined.
Fig. 2.18 In structural analysis the complete structure is broken down into two-dimensional components and the internal forces in these are subsequently calculated. The diagram shows the pattern forces which result from gravitational load on the roof of a small building. Similar breakdowns are carried out for the other forms of load and a complete picture is built up of the internal forces which will occur in each element during the life of the structure.
In large, complex, statically in determinate structures the magnitudes of the internal forces are affected by the sizes and shapes of the element cross-sections and the properties of the constituent materials, as well as by the magnitudes of the loads and the overall geometry of the structure. The reason for this is explained in Appendix 3. In these circumstances the analysis and element-sizing calculations are carried out together in a trial and error process which is only feasible in the context of computer-aided design.The different types of internal force which can occur in a structural element are shown in Fig. 2.19. As these have a very significant influence on the sizes and shapes which are specified for elements they will be described briefly here.In Fig. 2.19 an element is cut through at a particular cross-section. In Fig. 2.19 (a) the forces which are external to one of the resulting sub-elements are marked. If these were indeed the only forces which acted on the sub-element it would not be in a state of equilibrium. For equilibrium the forces must balance and this is clearly not the case here;an additional vertical force is required for equilibrium. As no other external forces are present on this part of the element the extra force must act on the cross-section where the cut occurred. Although this force is external to the sub-element it is an internal force so far as the complete element is concerned and is called the ‘shear force’. Its magnitude at the cross-section where the cut was made is simply the difference between the external forces which occur to one side of the cross-section, i.e. to the left of the cut.
Fig. 2.19 The investigation of internal forces in a simple
beam using the device of the ‘imaginary cut’. The cut
produces a free-body-diagram from which the nature of the
internal forces at a single cross-section can be deduced.
The internal forces at other cross-sections can be
determined from similar diagrams produced by cuts made
in appropriate places. (a) Not in equilibrium. (b) Positional
equilibrium but not in rotational equilibrium. (c)
Positional and rotational equilibrium. The shear force on
the cross-section 1.5 m from the left-hand support is
15 kN; the bending moment on this cross-section is
22.5 kNm.
Once the shear force is added to the diagram the question of the equilibrium of the sub-element can once more be examined. In fact it is still not in a state of equilibrium because the set of forces now acting will produce a turning effect on the sub-element which will cause it to rotate in a clockwise sense. For equilibrium an anti-clockwise moment is required and as before this must act on the cross-section at the cut because no other external forces are present.The moment which acts at the cut and which is required to establish rotational equilibrium is called the bending moment at the cross-section of the cut. Its magnitude is obtained from the moment equation of equilibrium for the free-body-diagram. Once this is added to the diagram the system is in a state of static equilibrium, because all the conditions for equilibrium are now satisfied(see Appendix 1).
Shear force and bending moment are forces which occur inside structural elements and they can be defined as follows. The shear force at any location is the amount by which the external forces acting on the element, to one side of that location, do not balance when they are resolved perpendicular to the axis of the element. The bending moment at a location in an element is the amount by which the moments of the external forces acting to one side of the location, about any point in their plane, do not balance. Shear force and bending moment occur in structural elements which are bent by the action of the applied load. Beams and slabs are examples of such elements.
Fig. 2.20 The ‘imaginary cut’ is a device for exposing
internal forces and rendering them susceptible to
equilibrium analysis. In the simple beam shown here shear
force and bending moment are the only internal forces
required to produce equilibrium in the element isolated by
the cut. These are therefore the only internal forces which
act on the cross-section at which the cut was made. In the
case of the portal frame, axial thrust is also required at the
cross-section exposed by the cut.
One other type of internal force can act on the cross-section of an element, namely axial thrust (Fig. 2.20). This is defined as the amount by which the external forces acting on the element to one side of a particular location do not balance when they are resolved parallel to the direction of the element. Axial thrust can be either tensile or compressive.
In the general case each cross-section of a structural element is acted upon by all three internal forces, namely shear force, bending moment and axial thrust. In the element-sizing part of the calculations, cross-section sizes are determined that ensure the levels of stress which these produce are not excessive. The efficiency with which these internal forces can be resisted depends on the shape of the cross-section.
The magnitudes of the internal forces in structural elements are rarely constant along their lengths, but the internal forces at any cross-section can always be found by making an ‘imaginary cut’ at that point and solving the free-body-diagram which this creates.Repeated applications of the ‘imaginary cut ’technique at different cross-sections (Fig.2.21), allows the full pattern of internal forces to be evaluated. In present-day practice these calculations are processed by computer and the results presented graphically in the form of bending moment, shear force and axial thrust diagrams for each structural element.
Fig. 2.21 The magnitudes of internal forces normally vary
along the length of a structural element. Repeated use of
the ‘imaginary cut’ technique yields the pattern of internal
forces in this simple beam.
The shapes of bending moment, shear force and axial thrust diagrams are of great significance for the eventual shapes of structural elements because they indicate the locations of the parts where greatest strength will be required. Bending moment is normally large in the vicinity of mid-span and near rigid joints. Shear force is highest near support joints. Axial thrust is usually constant along the length of structural elements.
4.4 Element-sizing calculations
The size of cross-section which is provided for a structural element must be such as to give it adequate strength and adequate rigidity. In other words, the size of the cross-section must allow the internal forces determined in the analysis to be carried without overloading the structural material and without the occurrence of excessive deflection. The calculations which are carried out to achieve this involve the use of the concepts of stress and strain. In the sizing calculations each element is considered individually and the area of cross-section determined which will maintain the stress at an acceptable level in response to the peak internal forces. The detailed aspects of the calculations depend on the type of internal force and, therefore, the stress involved and on the properties of the structural material.As with most types of design the evolution of the final form and dimensions of a structure is, to some extent, a cyclic process. If the element-sizing procedures yield cross-sections which are considered to be excessively large or unsuitable in some other way, modification of the overall form of the structure will be under taken so as to redistribute the internal forces. Then, the whole cycle of analysis and element-sizing calculations must be repeated.If a structure has a geometry which is stable and the cross-sections of the elements are sufficiently large to ensure that it has adequate strength it will not collapse under the action of the loads which are applied to it. It will therefore be safe, but this does not necessarily mean that its performance will be satisfactory (Fig. 2.22). It may suffer a large amount of deflection under the action of the load and any deformation which is large enough to cause damage to brittle building components, such as glass windows, or to cause alarm to the building’s occupants or even simply to cause unsightly distortion of the building’s form is a type of structural failure.

collapse, but excessive flexibility can render it unfit for its
purpose.
The deflection which occurs in response to a given application of load to a structure depends on the sizes of the cross-sections of the elements6and can be calculated once element dimensions have been determined. If the sizes which have been specified to provide adequate strength will result in excessive deflection they are increased by a suitable amount. Where this occurs it is the rigidity requirement which is critical and which determines the sizes of the structural elements. Rigidity is therefore a phenomenon which is not directly related to strength; it is a separate issue and is considered separately in the design of structures.
5. Conclusion
In this chapter the factors which affect the basic requirements of structures have been reviewed.The achievement of stable equilibrium has been shown to be dependent largely on the geometric configuration of the structure and is therefore a consideration which affects the determination of its form. A stable form can almost always be made adequately strong and rigid, but the form chosen does affect the efficiency with which this can be accomplished.So far as the provision of adequate strength is concerned the task of the structural designer is straightforward, at least in principle. He or she must determine by analysis of the structure the types and magnitudes of the internal forces which will occur in all of the elements when the maximum load is applied. Cross-section shapes and sizes must then be selected such that the stress levels are maintained within acceptable limits. Once the cross-sections have been determined in this way the structure will be adequately strong. The amount of deflection which will occur under the maximum load can then be calculated. If this is excessive the element sizes are increased to bring the deflection within acceptable limits. The detailed procedures which are adopted for element sizing depend on the types of internal force which occur in each part of the structure and on the properties of the structural material.




















Currently have 0 comments: